© Martin Gregorie, 2002, 2016, 2022
This paper arose from a seminar at the 2002 ITDG Associates Open Day on low cost energy sources for isolated villages. The presentation made the case that the use of small 200-300 watt wind turbines, providing power via battery banks for high efficiency lighting, radio and TV reception was cost effective in isolated communities located in areas with suitable wind speeds throughout the year. The turbines are two or three blade machines in the 2-3 metre diameter range. This size of machine is affordable, easy to transport via pack animal or bicycle trailer and easy to install on a light-weight wire braced mast. They can be built and maintained by local mechanics and electricians, thus providing local employment. These assumptions have been validated by pilot installations in Sri Lanka and Peru.
After the seminar I was able to examine an example machine. I was impressed by the mechanical and electrical design. It is difficult to see how that could be further improved. However, it did seem to me that the turbine aerodynamics could be made more efficient with little impact on the cost or ease of construction. This paper presents my thoughts on raising the turbine's aerodynamic efficiency.
I was a competitive model flyer, constructor and designer for 30 years before changing track and becoming a glider pilot for the next 20 years. Both of these activities have given me access to material that is apparently little known outside these interest groups.
Full size aviation has moved on to the regime of the very large and the very fast. Mainstream research has followed this trend and is generally not interested in the flow regimes that interest us. As a result, most recent low speed aerodynamics research has been carried out within the modelling community and the results have been published in modelling symposia and magazines. The same holds true for the gliding movement. Here the research has traditionally taken place within the Akaflieg movement, which exists within the German university system, and published in soaring journals and magazines.
What follows is an attempt to provide references to material that may not be widely known outside the model flying and gliding fraternities.
A wind turbine is closely related to a propeller, so anything that makes a propeller more efficient is applicable to a wind turbine as well. In both devices the blades act as flying surfaces, generating lift and drag just as a wing does. Unlike a wing, where all points along the semi-span operate at similar flow velocities, in a propeller or turbine the flow velocity varies with the position along the blade. This, however, does not affect the argument. It just makes matching the blade section to the operating conditions that much harder.
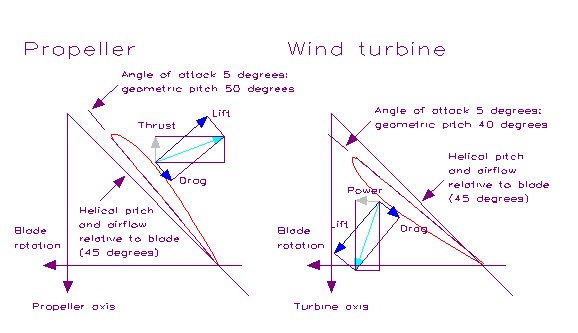
The most obvious difference between a propeller and a turbine is that a propeller is driven by a power source to create thrust. Thrust is proportional to those parts of the lift and drag vectors, generated by the blade, that are oriented into the air stream. In consequence the top of the airfoil also faces into the air stream. An increase in the blade's angle of attack is achieved by increasing the geometric pitch of the blade. A turbine, on the other hand, is driven by the airflow in order to generate power. Similarly to a propeller the power output is proportional to those parts of the lift vector, generated by the blade, that are oriented parallel to the turbine disk and directed in the same direction as turbine rotation. In consequence the top of the airfoil is oriented away from the air stream. An increase in the blade's angle of attack is achieved by decreasing the geometric pitch of the blade. This is hard to describe in words but easy to visualise; the following diagram should make this clearer:

The force diagrams alongside the blade show the resultant of the blade lift and drag vectors. The resultant is decomposed into the propeller thrust vector (parallel to the axis) and the turbine power output vector (parallel to the turbine rotation).
The issues listed below must be considered in optimising both propellers and wind turbines. They are listed in order of decreasing benefit:
The following assumptions have been used in developing the approach presented below:
I've grouped references that I consider useful for low-speed aerodynamics, i.e. that work at Reynolds numbers between 50,000 and 200,000, under the general headings of pitch distribution, wing sections, and wing shapes. This is the design range for a 2 or 3 metre diameter wind turbine. References and web sites that cover more than a single topic appear in each relevant section. Finally, I've added a section covering a suggested approach to optimising turbine blade aerodynamics.
From the comments in the introduction it follows that an optimised pitch distribution calculated for a propeller of similar geometry can only be applied to a wind turbine by:
The straight forward approach to designing a propeller or turbine is to determine the required blade pitch from the design airspeed and rotational speed and then set the blade pitch along the blade using a helical distribution. However, although this will work it's not particularly efficient. Specifically, it has ignored the characteristics of the blade section and losses at either end of the blade.
The problem with using a helical pitch distribution is that it is only optimal when the blade is doing no work. Extracting work from it requires that the blade has a positive angle of attack, which can be achieved by slowing the turbine's rotational speed, but the resulting pitch distribution is only optimal at one point along the blade. At all other points the blade is doing less work than it is capable of, resulting in an overall lower power output.
An immediate improvement in output should be obtained by determining the angle at which the Cl/Cd ratio of the blade section is maximised and subtracting this from the helical pitch at all stations along the turbine blade. The improvement results from ensuring that the blade section is operating at its most efficient angle of attack under a wide range of conditions. Model propellers designed using this principle have shown good properties over a wide range of operating conditions, though for a propeller the angle of attack is added to the helical angle. See the previous diagram for clarification on this point.
The final touch is to adjust the pitch distribution along the blade to minimise losses at the root and tip. A simple approach is to ignore blade root losses and to reduce the angle of attack progressively over the outer 10% of the blade. The pitch reduction should be 2 degrees at the tip.
Professor Eugene E. Larrabee is probably the most influential propeller theorist when it comes to high efficiency propellers intended for use at relatively small Reynolds numbers. He had a major influence on the design of propellers used by virtually all successful human powered aircraft. He is an ex-model flyer and his design method is the basis of many of the propellers used in the international F1B class for rubber powered competition aircraft. F1B represents the highest level of development in this arena and hence is a good proving ground for propeller theory.
The fullest optimisation will result if the Larrabee design method is applied. This determines the optimum pitch and chord distributions over the whole blade, thus also determining the best blade shape for the specified working conditions.
Blade or wing sections are designed to operate at specific flow regimes which are best characterised by the Reynolds Number (Re), a dimensionless value that links air density and viscosity, the chord length of the section and the airspeed at the design operating conditions:
Re = rho / mu * V * c
where:
| rho | density of air (kg/m3) |
| mu | viscosity of air (kg/m/sec) |
| V | airspeed (m/sec) |
| c | section chord (m) |
At sea level this approximates to:
Re = 68459 * V * c
What little theory and actual data on wing sections exists that is suitable for our velocity range (Re 50,000 - 200,000) either dates from the first quarter of the 20th century or has emerged from model flying development. In particular, the results of reliable unclassified wind tunnel tests on wing sections suitable for operating in this flow regime have all been published by model flyers for model flyers. Sections developed for use on manned aircraft, excluding human-powered types, all operate at Re numbers above 1,500,000 and are quite unsuitable for the flow regime of interest to us.
Note that airfoils designed to work above Re 150,000 are invariably flat bottomed or semi-symmetrical. As the velocity drops toward Re 75,000 the addition of top surface turbulators becomes beneficial. As the Re number drops still further the sections tend to become thinner and undercambered sections become progressively more attractive. Undercambered sections have concave under surfaces. Top surface turbulation becomes beneficial - typical turbulation schemes involve 0.5mm threads at 5% chord and at the upper surface high point. The limiting case is reached in the Re 10,000 region, where the optimum section is a 5% cambered curved plate. Below this the optimum camber continues to drop until at Re 3,000 the flat plate becomes optimum. This is the flight regime for large insects such as Monarch butterflies.
The blade (wing) shape, which defines the amount and distribution of sweep-forward, sweep-back and taper ratios, can have quite an influence on wing performance. The first reference in this section gives the development of the Schumann shape. This was immediately successful on the Schlemp-Hirth Discus, a 15m standard class competition glider and has since spread to the model world and to small, subsonic airliners, such as the Dornier 328. Its success is due to its ability to control the spanwise flow that forms above the trailing edge of a wing by ensuring that the flow is toward the tip. Flow toward the root is harmful for an aircraft since it grossly disturbs the airflow at the wing root, causing large amounts of drag. It would seem likely that it has equally harmful effects on a turbine blade's efficiency.
A correctly shaped blade tip can have a beneficial effect on blade efficiency. A good tip shape is one that moves the tip vortex as far outboard as possible, stabilises its position and minimises its size.
The well-known NACA tiplets fitted to late model Boeing 747s and other airliners are designed to do just this, but do not work well at the chord sizes we are using. Their setting angles are very critical, they are fragile and the Re numbers we work at are too low for them to be efficient.
The Hoerner tip is a more interesting approach. It is simply a tip shaped according to the following rules:
The following photographs show two different Hoerner tips. The DG505 is a high performance dual seat glider. The last photograph shows the tip on one of my F1A class model gliders:
 |
 |
|
DG505 tip plan view. The trailing edge is actually straight. The apparent curve is due to the camera angle. The tip chord is about 350 mm. |
DG505 tip showing the curved trailing edge. The tip curves upwards to provide ground clearance when, as now, the glider is resting on a small skid under its wingtip. The trailing edge rises more than the leading edge so the tip is washed out. |
 |
|
This tip has a chord of 100 mm. Note the sharp edge on the tip where the upper surface curves down to meet the lower surface. The trailing edge is parallel to the wingspan while the leading edge has a sweep of 9.5 degrees. This wing is designed to work at a Re of 50,000, hence the textured surface and thread turbulators, which work well in this airflow regime. The Hoerner tip is carved and sanded from a balsa block which is covered with 25 gsm glass cloth adhered with three coats of cellulose nitrate model dope. |
There are many variations on this theme:
The simplest way to improve aerodynamic efficiency of a typical 2 metre diameter three bladed turbine would be to select an airfoil that is well suited to the operating conditions, improve the pitch distribution by using the helical + angle of attack distribution and change the tip to a simple Hoerner shape. This is a minimum effort approach that should produce a noticeable performance improvement. The steps are:
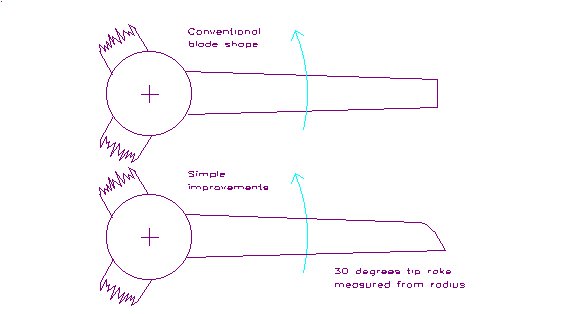
This is the same as Simple improvements except that the blade shape is further modified. Step 4 becomes:
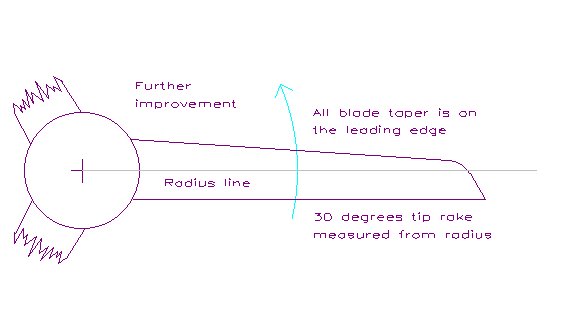
The effect of this change is to further reduce tip losses by influencing airflow along the blade. Its effect may be fairly marginal.
This uses the full Larrabee method to determine pitch distribution and blade shapes that are well-matched to the design operating conditions. Steps 1 and 2 are the same as above:
The blade shape derived from the Larrabee method will have a reduced chord at root and tip. The maximum chord will move to around 30% of the blade radius. These changes will make the master blade rather harder to carve accurately. However, once the moulds have been taken from the master blade the remaining production steps should not be greatly affected.